Math Showcase Piece

What is good fellas. In today’s Gary’s Substack post, we’ll be taking a look at some past tests, and correcting them to show Mrs. Zorzitto that I have learned from my mistakes. Also, sorry Zander Li for letting you down, man. I originally planned on doing an epic parody of Outkast’s Ms. Jackson. It started like this:

Sorry Zorzitto (ooo)

I am for real

never meant to mess your test all up

I apologize a trillion times

And some more really hood stuff. I realized although I’m hood and gang, I didn’t have enough time (in hours) to complete a rap of my finest work, which is why I will be doing my math showcase piece through the medium of Substack. The first test I’d like to correct is the Unit 3 Quadratics Functions test.

Quadratics Functions Test

The first question I got wrong was question one:

I did not simplify the fraction properly. The fraction (16 + 4√15)/(24) could be further simplified by factoring out 4, turning the fraction into (4(4 + √15))/24, which is (4 +√15)/6. Hooray. By the way, for these questions I got wrong by not simplifying that also have two solutions, I’ll just be fixing one of the solutions. Anymore would be unhelpful for the purpose of the assignment.

Question 1c). I got it wrong, again, for the same reason.

In question two, I made a similar mistake, once again not simplifying a final answer. (-4 - 2√10)/-4 should have been simplified to (-2(2 + √10))/-4. Then, we can divide the numerator and denominator by -2, getting us the final answer of (2 + √10)/2.

Then in question 2, I lost half a mark making the same mistake again:

Done properly, (-4 - √56)/10 should become (-4 - 2√14)/10, then -2 could be factored out, and then dividing the numerator and denominator once more by 2. We would end up with -(2 +√14)/5.

In the next question, I received a “?”, which hurt my feelings greatly originally (not anymore) (I don’t care) (I am okay) (It’s just one question) (Grades don’t determine my future) (I can change and improve my mathematics abilities through rigorous training) (I am a capable human being):

But through rigorous studying and examination, I can finally solve this problem correctly:

Then in question 6, I failed to understand that the +3 at the end of the equation is not the y-intercept. Additionally, I used the two coordinates’ two x points as roots, when they are not:

Here is how I’d do it now with a more developed cranium:

In question 7, I made a foolish mistake of doing 4*2 = 6. It should’ve been 8, making the fraction 81/8.

The correct answer would’ve been that the max area of the rectangle is 81/8cm^2. (81/8 cannot be further simplified).

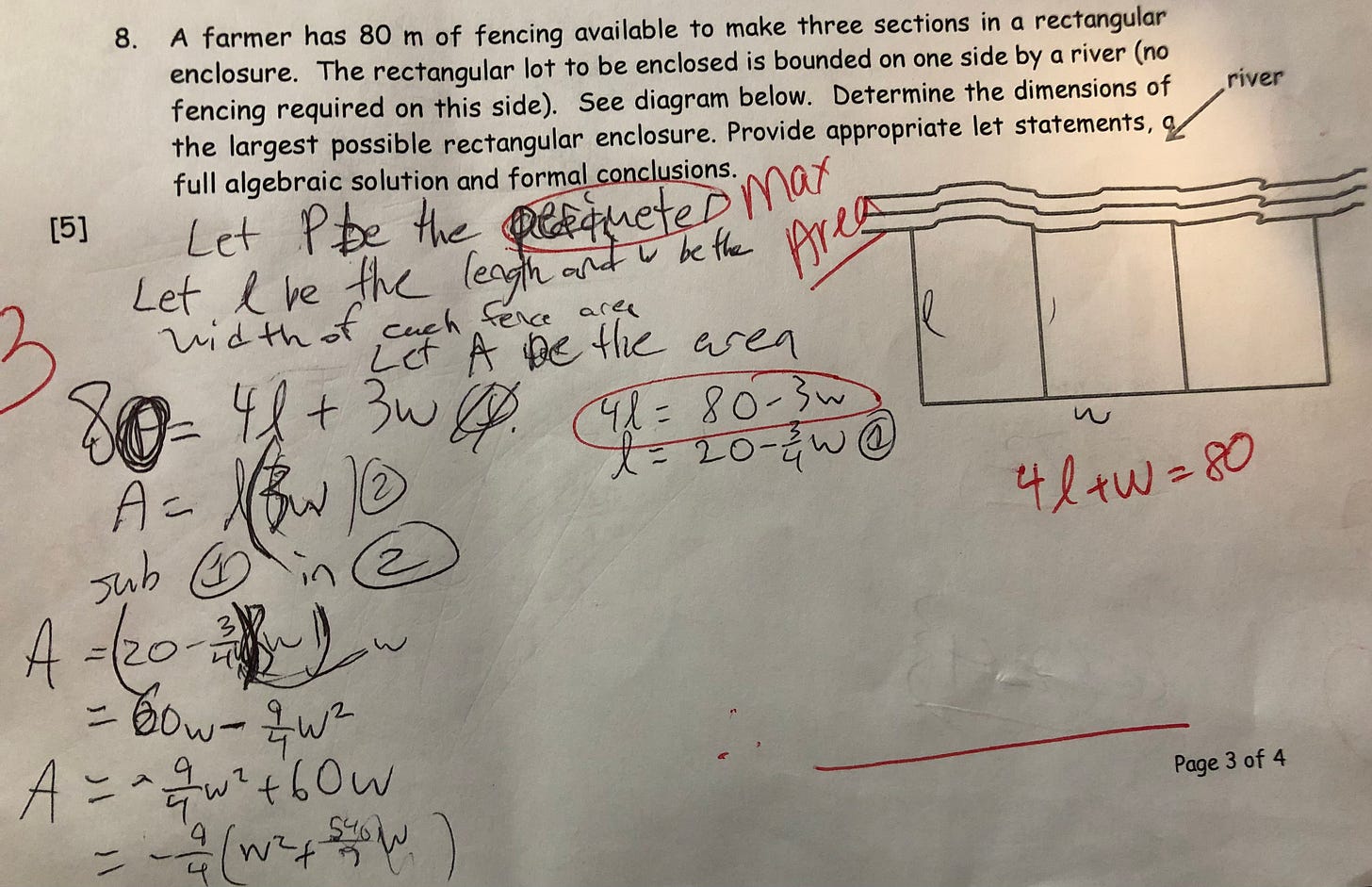
In question 8, I mistakenly let “P be the perimeter” (Zhang 3), when I did not need to solve for the perimeter. The 80m of fencing was the total fencing available — not the perimeter. The equation I made of 80 = 4l + 3w was also not even correct. I should have made two equations. One being A = lw, and the other being 4l + w = 80. Then I would be able to sub them into each other, to get a quadratic function, and getting the width at the same time. This mistake showed my lack of understanding of word problems.

Here is how I’d solve it now:

In question 9, I used addition instead of subtraction. Should have been easily avoidable, but I didn’t catch it:

It should have been “-” because if it was (x + (4 - √7)/3)(x + (4 - √7)/3), x would have to equal negative (4 - √7)/3, which is unlike the described roots. Here’s how it’d be, done correctly:

On question 10a). I only got part marks as I didn’t have enough time to complete the question properly. I missed the whole b^2 - 4ac = 0 for there to be one solution. I also got question 10b. and 10c. completely wrong, although c = 72 is a pretty darn good guess, in my opinion.

Here is how I’d solve the problem now:

Many of the marks I lost from this test came from goofy mistakes, but also from simply not knowing how to solve problems. This likely happened due to a lack of studying and preparation. I have since started preparing and studying smarter, and more for tests.

Identity Quiz

I got the first question wrong because I did cosx = 1 - sinx, and 1 + sinx = cosx, showing my misunderstanding of the Pythagorean identity.

I now understand that this identity cannot be rearranged the way I did, and the proper way to prove this identity would be like this:

I got the second question wrong because I turned tan^2x into sin^2x / cosx, which is not correct.

Here’s the proper solution to this one:

I got question four wrong. I did not recognize that cot^2x + 1 = csc^2x, which would have made me been able to solve:

Had I recognized the rearrangement of the Pythagorean identity, my solution would have been:

Before writing the quiz, I didn’t study or review, and so I didn’t remember the basic trig identities, and I didn’t remember the Pythagorean identities. I did get lucky when I randomly decided that 1/sinx = cscx, and 1/cosx = secx, allowing me to get at least a few marks. My poor mark on this quiz was because I just did not do the necessary preparation for the quiz. The next unit test we had, I got full marks on the two trig identity problems, because that time I learned the identities beforehand.

Unit 5 Test: Transformations

First question I got wrong on this test was me forgetting to factor to get rid of the RED FLAG!!!!!

When factored correctly, the exponent is -2(x-2), and the horizontal shift is 2 units right.

I got question 7 wrong, making the mistake of placing the exponent within the brackets. In part b of the question, I made the mistake of getting the sign wrong in the domain.

The domain should be: D = {x|x≤5, x∈ℝ}. The exponent of ^2 should be outside of the bracket because it must apply to both the 1/2 that has been factored out.

Okay I got question 8 wrong as well, making a mistake with transformations.

Here is what the new the equation actually is:

Concluding

The three tests I’ve corrected in this Showcase Piece show my lack of preparation, and carelessness whilst writing. Although I’ve made many mistakes in my tests so far in the course, my scores have been getting steadily better and better. The last two test I wrote, I got a 94, and a 100, which is far higher from the original low marks I was getting at the start of the course. I think doing more CYUs has helped me greatly, and continuing to do even more CYU would continue to help me get better at math. Because quite frankly, sometimes I would not fully understand a key concept, so when I would do CYU questions, I’d be able to solve them, but without a real understanding. So later on a test with harder questions, I wouldn’t know how to solve it because of my lack of attempt at understanding everything about the unit’s content. I hope to continue to improve my mathematics skills through more practice and studying, and get a 100 on the exam.